论文笔记：几何等变图神经网络综述

发表于 2023-06-03 更新于 2023-10-18 分类于文献阅读阅读次数：本文字数： 13k 阅读时长 ≈ 23 分钟

Geometrically Equivariant Graph Neural Networks: A Survey

摘要

许多科学问题需要应对几何图(geometric graphs)的数据格式。不像传统的图数据，几何图具有平移(translation)、旋转(rotation)、(或)反射(reflection)的属性。研究人员利用这样的归纳偏置并开发了几何等变的图神经网络，它可以更好得学习几何图的几何和拓扑结构。尽管研究如火如荼，但是对于该领域仍然缺少一个全面的综述来总结等变GNN是如何运算的，这一不足阻碍了等变GNN的发展。为了这个目的，我们精简了必要的数学表达，通过分析，根据GNN中的信息传递和聚合过程，将现有方法分为了3类。我们也总结了领域内的基准数据集，以加快方法开发和实验评估。最后，我们展望了未来的发展方向。

引言

许多问题尤其是物理学和化学中都需要处理几何图的数据。不同于一般的图数据，几何图中每个节点不仅有属性特征，还有一个几何向量。例如，一个分子/蛋白质就可以视为一个几何图，其3D坐标的位置即为几何向量；或者在一个量子多体系统中，3D状态(位置、俗定和自旋)为粒子的几何向量。值得一提的是，几何图具体平移、旋转、(或)反射的对称性，这是由于不管我们如何平移或旋转粒子，物理定律限制了粒子的动态变化导致它们永远是不变的。当面对这种数据时，很重要的一点就是将对称性的归纳偏置引入到模型设计中来，这也是几何等变图神经网络的动机。

GNNs最早由 Sperduti 和Starita在1997年提出，现在随着深度学习的发展GNN在图数据建模上具有其它方法不可超越的优点。尽管许多学界提出了许多模型架构，但之前大部分GNNs都不是几何等变的，这使得其在几何图上的表现不是最佳。为了获得几何等变性，许多工作通过改进GNN中的信息传递和聚合，包括在SE(3)群上(即3D平移和旋转变换的集合)等变的TFN，Lie群上(3D平移和旋转以及更多的可微变换集合)的LieConv，包括平移、旋转和反射的n维欧式变换集合上的EGNN。

考虑到目前的有成效的研究成果，现在仍没有一个描述等变GNN是如何处理数据的综述文章。这不仅阻碍了其它领域研究者快速进入等变GNN的领域，也可能阻碍该领域进一步的创新和发展。因此，我们通过这篇综述来系统全面地介绍几何等变GNNs，详述目前领域解决的问题以及未来的发展方向。我们的贡献如下：

容易上手。我们只提供了必要的数学表达，包括等变性、群、群表示的定义。我们尝试去使数学部分完善而简要，以免任何多余的符号混淆读者。更重要的是，所有模型都以一个通过的符号来表示，如此这般读者可以很轻松分辨不同模型之间的差异。
新的分类方法。我们提出了一个新的方法来分类等变GNNs。通过关注信息传递和聚合的方式，我们将等变GNNs分为3种形式：不可约表示(irreducible representation)，正则表示(regular representation)和标量化(scalarization)。
丰富的资源。除了方法，我们还探究了目前研究的应用广度。我们根据数据类型和模型任务列出了完整的基准。这可以为模型开发、实验评估和比较提供便利和指导。
未来展望。我们提供了对当前前沿工作的分析，并讨论了未来理论和实践上的研究方向。特别地，我们展望了四个方面：理论完整性、可扩展性、层次性和更多真实世界的应用及数据集。

背景

信息传递 GNNs

GNNs被广泛提出来解决关系数据。在一个图上，和分别是节点和边的集合。每一个节点都被赋予一个特征对每个节点来说表示为。同时，图上也可以由边特征，即节点和连边的特征为。最早的信息传递架构是为了将重要的GNNs进行统一。对每个节点或者边，其迭代式计算节点信息和并聚合邻居信息，可以表示为：

其中，是节点的邻居集合(默认没有自环)，和是参数函数。

Eq.(1-2)中描述的一个有趣的属性是GNN有置换等变性(permutation equivariance)，因为是置换等变的(即node-order equivariance)。现代GNNs实际上就是为了解决这个问题来设计的。一些工作在复杂系统上使用GNNs，并输入几何信息，如粒子的3D坐标。DPI-Net构建了一个动态互作图，其依据是物理模拟器天生是来学习粒子动力学。HRN同样设计了一个互作图来捕获复杂物体的关系，只不过是一个层次化的方式，动力预测也就更精准。除了手动指定模拟互作的图，NRI自动从潜在互作图中推断，并在多体粒子系统以及人类动作捕捉中取得了不错的性能。这些工作都证明了GNNs在模拟几何系统中的优越性，因此其具有置换等变性，所以可以减少输入顺序的组合复杂性。Townshend的工作使用3D GNN来预测分子性质。不过，在本文中我们关注几何性质以及欧式空间中的等变性，而不是置换群。对于上述方法，它们仍欠缺发现几何相似性在3D空间的作用。我们将介绍什么是几何等变性，并且解释为什么需要这个性质。

等变性

假定和分别为输入和输出的向量空间，而且两者都被施加了一系列的变换：和。函数如果我们对输入施加任何变换，输出也相应跟着进行相同的变换或者以一个可预测的方式来变换即被称为相对于等变的。形式化以后，我们有：

定义 1 (等变性) (Equivariance)

如果中的任何变换满足函数，则其是-等变的其中和分别是输入和输出的群表示。具体地，如果 $是相等的话，$ 是等变的。

定义 2 (群) (Group)

一个群是一系列变换的集合，其中是二元运算，满足下列属性：在任何复合运算下都是闭合的，而且存在一个恒等元素(identity element)，每一个恒等元素都有一个逆(inverse)。

考虑到上述群的定义，下面是一些例子：

是n-维正交群(Orthogonal group)，包括旋转和反射。
是特殊正交群(Special Orthogonal group)，包括旋转。
$是$ n-维欧式群，包括旋转、反射和平移。
是特殊欧式群，包括旋转和平移。
李群的元素是来自一个可微的流行。上述几个群都属于李群的具体例子。

群表示

一个群的表示为一个可逆的线性映射(invertible linear map)，即，输入一个群元素，然后作用在向量空间上，同时它也是线性的: 。例如，一个的矩阵表示为正交矩阵，且。这个是 Eq.3在的一个实例，如果输入和输出空间共享同样的表示即为。对于平移等变性，我们有且。

等变性(也叫协变性covariance)最早在物理学中引入来保留对称性。将欧式等变性加到现代深度学习框架中这个想法来自Cohen和Welling，他们将CNN的卷积算子推广到离散的旋转和反射子群中，他们的工作进一步引入可引导性(steerability)到卷积核中，将特征图的正则表示推广到了不可约(irreducible)和商(quotient)表示中。下面，我们将介绍如何将等变性推广到目前GNNs的信息传递中来。

几何等变GNNs

这一小节先描述了几何图的定义式，然后总结了处理这种数据的几何等变GNNs。

几何图(Geometric Graph)

在许多应用中，图不仅包括拓扑关系和节点特征，也包括了几何信息。以一个分子为例，每个原子都会赋予一个标量特征（如电荷、质量等等），也会赋予一个几何向量（如粒子的位置和速度坐标）。当使用GNNs来处理这种数据时，我们可以将等变的归纳偏置嵌到模型中。例如，当预测一个分子的能量时，我们需要输出一个不受到几何向量旋转影响的值，即旋转不变性；当预测分子动力时，我们需要输入具有对于原子位置的等变性。为了更好区分，我们将几何向量以粗体形式呈现，而非几何向量则为普通形式。

于是， Eq.(1-2)重新写为了：

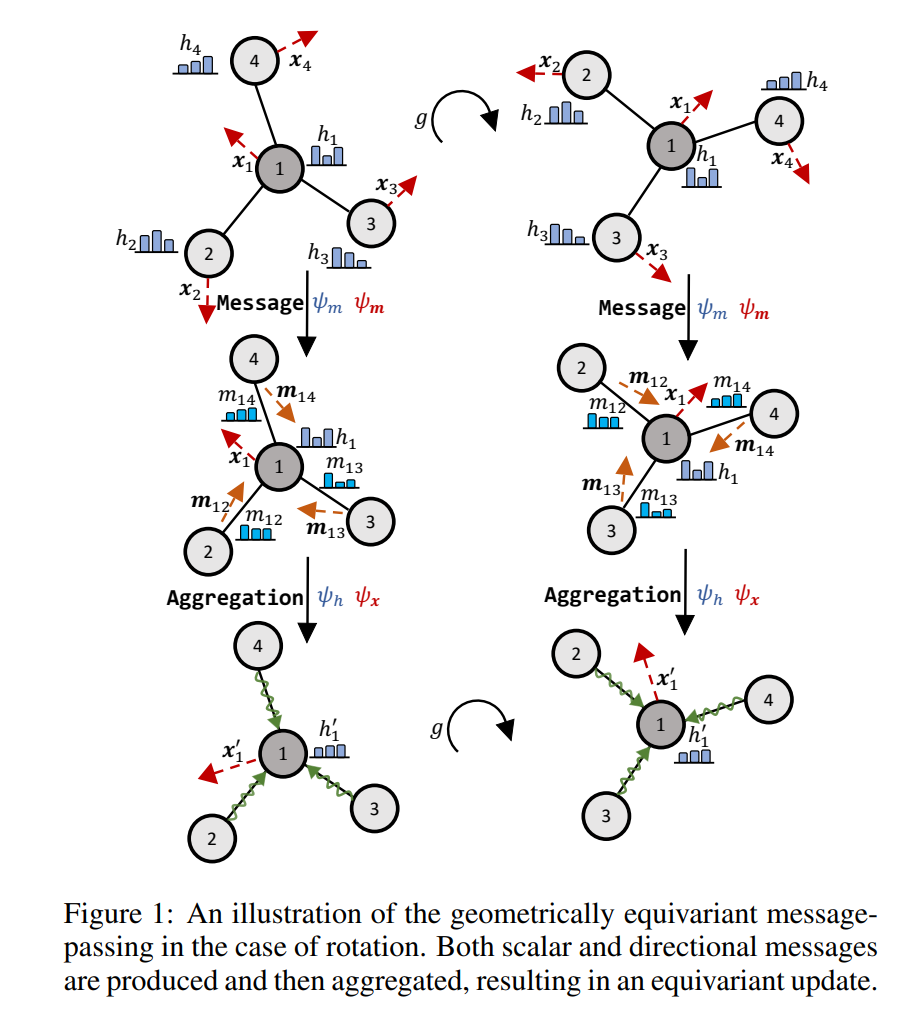
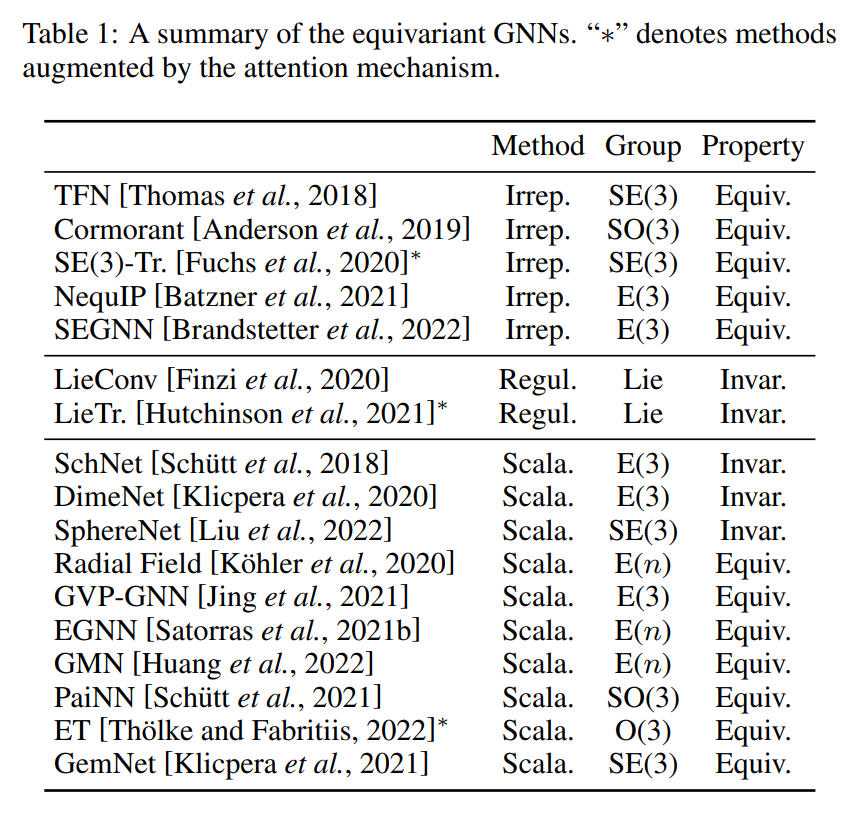
这里，和分别为在边上信息传递输出的标量和方向向量，和分别为对标量和几何向量的信息聚合函数。此外，对于输入是G-不变的，而对于输入是G-不变的；对于和是G-等变的。这个等变信息传递可以见图1 。

图1 Geometrically Equivariant Message Passing in the case of rotation

许多等变GNNs被提出，不过其差异通常在Eq. (4-7)的具体实现上，如不同的群，表1 总结了目前的等变GNNs。对于如何表示信息，我们将目前的方法分为了三种：不可约表示、正则表示和标量化。大部分情况下，平移等变性都很好满足，因为相对距离是平移不变的，如何在更新时进行残差求和又赋予了等变性。因此，我们接下来的讨论主要关注于旋转变换和其他变换。

不可约表示(Irreducible Representation)

根据表示理论，一个紧群(compact group)的线性表示即为对其不可约表示(缩写为irreps)的直接求和得到一个相似的变换。具体对于群来说，irreps是 Wigner-D矩阵。对于每个，有：其中，是Wigner-D矩阵，是正交矩阵表示基的变换，为直接求和或者矩阵沿对角线拼接。因此，向量空间被分为了个子空间，每一个都被所变换，第子空间中的向量被称为向量。例如，在我们的例子中，标量是含有个通道的type-0向量，是type-1向量。这些向量通过张量积互相作用，然后通过Wigner-D矩阵的张量积得到Clebsch-Gordan (CG) 相关系数，由CG分解所得：为群乘运算。

群要求一个集合，一个群乘运算，以及四个需要满足的条件：

封闭性：对群中任意两个元素，有；
结合律：对群中的任意三个元素，有；
单位元：群中存在且仅存在一个元素，使得任意一个元素$f G $有$ ef=fe=f$；
逆元：对群中任意一个元素，存在且仅存在一个元素，使。

构建等变信息传递的最后一个步骤是球谐函数，其为等变的基础。有了上述的构建元件，Thomas提出了一个满足SE(3)-等变的TFN层：

其中，表示度为的节点的几何向量，为节点坐标，为自作用权重，filter 是旋转可引导的(rotation-steerable)，表明对于任意旋转，满足。具体来说：

一系列可学习的半径函数，球谐函数，CG相关系数。更多细节参见Weiler et al.的文章。

TFN将视为的信号函数，计算只更新同时在所有层中固定。利用的可引导性(steerability)可以很容易检查的等变性。如果我们将自己视为一个函数，TFN分别实现了Eq. (4)和(6)，通过设置；以及Eq. (5)和(7)设置。

许多TFN的变体都被提出。Fuchs等进一步将注意力机制引入Eq. (10)，将乘以一个SE(3)不变的注意力。Dym和Maron理论上揭示了TFN和SE(3)-Transformer都是SE(3)-等变性函数的通用似然。Cormorant同样利用irreps但是Clebsch-Gordan是非线性的。NequIP进一步讲E(3)-对称性引入到原子间势能预测。最近Brandstetter的工作推广可引导向量，并建立一个E(3)等变的GNN，且具有可引导性。然而，这些方法的计算消耗仍然很大，限制了向量的使用。然而，irreps通常是表示于SO(3)群，而不适宜实现在其它群如E(n)中。

正则表示(Regular Representation)

另一种方法使用正则表示直接寻求在群卷积中获得等变性，其将卷积算子作为群上的函数。然而，当处理连续和光滑群时，群卷积的正数就变得难以处理，一个可行的方法是利用李代数。为了这个目的，Finzi et al.提出了LieConv，LieConv可以通过Lifting操作将输入映射到群中的元素，然后利用PointConv这一trick完成群卷积的离散化计算。特别地，利用我们的符号来说，LieConv可以写为：

其中，是的lift，对数log将每一个群成员映射到李代数 (向量空间)，而为参数化的MLP。此外，Eq. (13)通过除以节点数量来进行归一化，即。很明确LieConv只明确了节点特征的更新，同时保持几何向量不变，这意味着LieConv具有不变性。

通过相似的想法，LieTransformer使用了自注意力机制来动态得计算卷积核中的权重，以求提升模型的性能。因此等变性可以通过任意的李群或者其离散的子群，故基于正则表示的方法享有很高的灵活性。另一方面，由于离散化和采样，这一方法也在计算复杂度和性能之间达到了平衡。除非我们引入外部哈密顿动力学(Hamiltonian dynamics)来重新定义几何向量(如Finzi et al.)，否则这种方法的一个缺点就是我们很难将Eq. (12-13)推广到几何向量上来。

标量化(Scalarization)

除了群表示方法，许多工作采用一个通用的方法即标量化来建模等变性。通常来说，几何向量首先被转换成不变标量，之后再接几个MLPs来控制其量级，最终添加原先的方向以获得等变性。这个想法最早在SchNet和DimeNet提出，不过只具有不变性。SphereNet进一步在标量化的信息传递中添加了角度和扭转的信息，从而使得具有不变性的网络可以区分手性(chirality)。Radial Field实现了等变性的版本，不过只是在几何向量上进行运算，而没有考虑到节点特征。EGNN进一步以下面的范式更新了这个想法：

其中，是几何向量和的标量化形式；、和都是任意的MLPs。通过设置，EGNN同时传播了节点特征和几何向量，以等变的方式直接实现了Eq. (4-7)。这个方法的精髓在于构建不变的信息，然后沿着径向方向(radial dirction)重新转换回到等变的输出，与我们计算两个带电粒子的库伦力(重力)类似。注意Eq. (15)与Eq. (16)不同，Eq. (15)聚合了所有非节点邻居的信息，这也反映了每个节点都别其他所有节点影响的规律。

除了EGNN，GMN(Huang et al.)将聚合推广到多个几何向量上(例如位置、速度加上力)，标记为，表明实际上就是一个通用的形式。通过这个方法，Eq. (14-15)中的互作就可以扩展到空间中，以作为基础而不是只有径向一个方向。这一性质在约束系统中极为重要，因此系统中非径向信息向量(如角动量、扭矩)可能通过物体之间的互作而产生。尽管这一方法已经很简单了，但是Villar进一步给出了理论支撑，表明标量(内积)技巧是获得等变性的通用方法。GemNet利用这种普遍性加入了大量的几何信息，例如二面角，在信息传递中进一步改善了DimeNet。

我们对于Eq. (15)的解释为不变标量和等变向量的乘积仍可以产生一个等变的向量。在这个原则下，另一系列工作设计了不同的等变信息传递方法，如PaiNN和注意力等变Transformer(the attentive Equivariant Transformer)通过径向基函数加入原子间距离将不变的SchNet增强为等变的版本，并随着标量特征不断迭代更新向量。GVP-GNN利用了相似的想法，不过其理论上的普遍性要更强。

应用

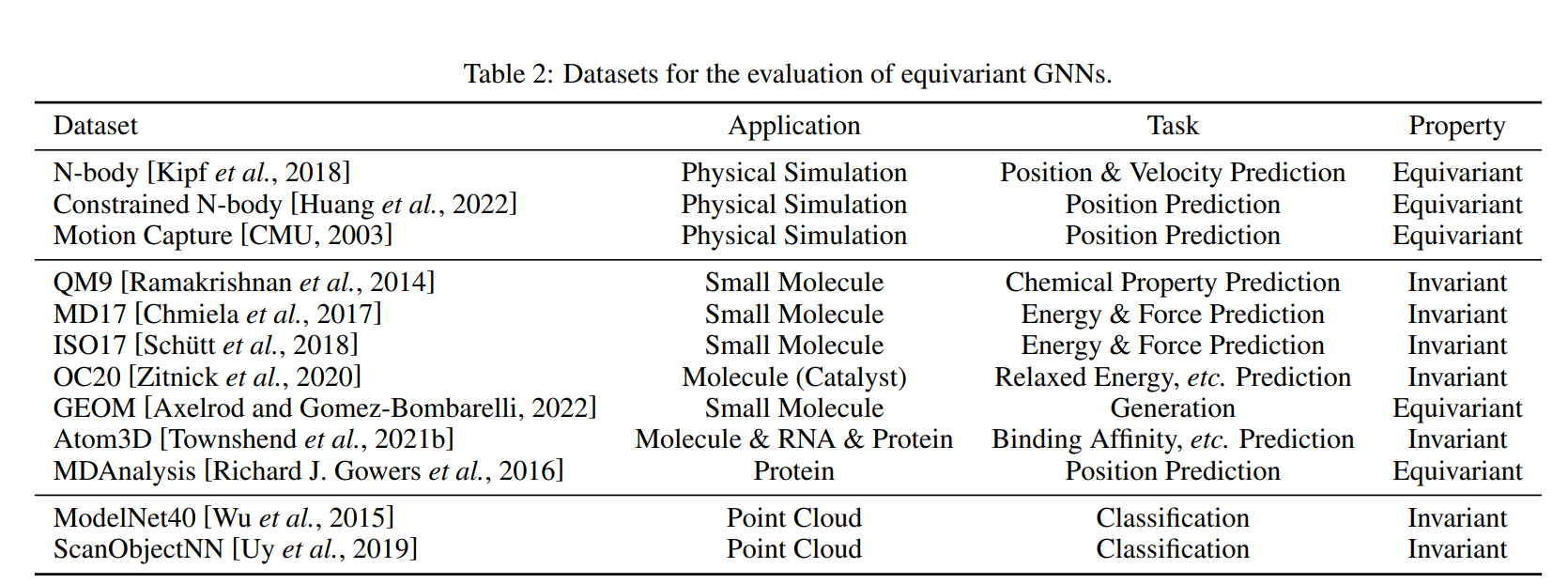
等变GNNs在许多真实世界的几何数据中都有广泛的应用，从物理系统但化学物质无一大放异彩。在本节，我们分别引入了物理系统、分子数据和点云的应用场景。表2提供了所有数据集的总览。

Datasets for the evaluation of equivariant GNNs

物理动力学模拟

模拟复杂物理系统的动力学一直以来都是一个富有挑战性的话题，近年来使用神经网络来推理系统中的互作关系和动力学。物理学系统内是一些如带电粒子的物体，它们在物理定律的约束下通过各种力相互作用。多体问题(N-body simulation)是许多带电粒子受到库仑力的作用，这个问题的目的是给定最初状态预测每个粒子的动力学变化，包括位置、速度和电荷。这样一个任务的E(3)等变的，因为粒子的动力学变化是随着整个系统来平移、旋转和反射的。SE(3)-Transformer和EGNN都证明了等变GNNs在这个任务上的效果。Huang et al.在系统中加入连接的刚体如棍和铰链，从而一个更有挑战性的问题即约束多体问题出现了。Brandstetter et al.不使用重力，并显著增加粒子数量创建了该系统的另一种形式。其他研究者也采用人类移动来捕获数据，其中包括了人类不同方向上的移动轨迹。

分子

另一个重要的应用场景就是分子数据，分子中的原子受到不同化学作用的影响。对于分子数据，标量节点特征通常是原子数量，而连边通常是化学键或者通过一个距离阈值来构建。我们总结了等变GNNs在分子数据的应用，包括了预测和生成。

预测

QM9是一个常用的数据集，其中包括了12个量子性质，是一个不变性的任务。MD17包括了8个小分子的分子动力学轨迹数据，能量和互相作用力为标签。与MD17类似，ISO17包括了129个同分异构物的短的动力学模拟轨迹。OC20数据集考虑了催化剂和吸附物之间的结合过程，任务包括预测相关的能量和给定最初结构预测结合后的结构。上述几何等变GNNs中，大部分工作都在这些数据集上有不错的性能，可以准确预测目标同时与传统方法相比计算开销大大减小。

此外，AlphaFold2在预测蛋白质结构上取得了优异的结果，也开启了化合物和几何等变性的结合。一些工作将等变GNNs如TFN推广到了大规模的分子系统如蛋白质中，而且采用层次化的方式对子结构进行采样。通过同时处理两个几何图，Ganea在刚体蛋白质蛋白质对接上也进行了尝试。ARES利用旋转不变网络处理了RNA数据，而且在18个RNA结构上训练的数据也有较好的泛化能力。数据方面，MDAnalysis提供了靠谱的蛋白质分子动力学的数据，Atom3D是一个包括8个分子预测任务的全面数据集(从小分子到RNA到蛋白质均有涉猎)，其中包括了分子几何信息。

生成

前人将大量未标注的数据分为了两个子集GEOM-QM9和GEOM-Drugs。这些数据集包括了大量的小分子构象样本，而且可以利用在分子构象生成的无监督训练中。ConfGF和DGSM使用旋转-平移等变的GNN，确定了基于分数的生成模型的分数函数的参数，得到一个可以学习构象的条件分布的生成模型。GeoDiff进一步将生成模型扩展到了扩散模型，同样在等变GNN的保证下使用了扩散核。此外，Equivariant Flow证明了使用等变核构建归一化的flow在密度变化情况下的可行性。然而，只有坐标被考虑进节点特征。之后有人利用EGNN作为核，然后在连续归一化flow动力学中同时建模了向量和标量输入的进化。这些方法都可以进行无条件的生成，构象可以在没有提供分子图的条件下进行生成。

点云

点云是表示一系列有坐标的物体。ModelNet40和ScanObjectNN是两个常用的点云数据物体分类数据集。因为点云数据中节点的连接关系未知，所以等变GNNs中使用的邻居通常为，为最大距离。TFN和SE(3)-Transformer都可以在点云数据集上取得不错的效果。最近，Chen提出了针对点云的SE(3)等变的卷积方法，可以迭代式进行群卷积和点卷积。这些方法都证明了等变GNN相较于传统3DCNN的优势，因为不需要体素化/网格化(voxelization/rasterization)将数据表达到欧氏空间中，而且还能保住等变性。

未来研究方向

理论完整性

不像其余GNN理论框架，具有一套很好的表达能力和泛化能力描述方式，GNNs等变性这一方面略显不足。尽管有些工作分析了一些方法的普遍适用性，他们的讨论也仅仅停留在信息传递上面，而整个图模型的属性仍然未知。如果能够探究现存理论框架，并加以分析为何其可以建构起如此强大的等变GNNs，那将会是一个有意思的话题。

延展性

如3.几何等变GNNs中所说，利用群表示理论的方法需要巨额的计算开销，限制了其在大的复杂系统如蛋白质上的延展。如果加上注意力机制后，这个问题就特别验证。因此，目前急需在等变信息传递这一方面加快计算，可能的解决方法是利用似然和有效的采用来保证可延展性。

层次化结构

许多现实世界的系统都是层次化的。例如，有机分子有许多功能团组成，而蛋白质由氨基酸组成。利用这种层次化的关系，我们有可能利用等变GNNs来建模不同细粒度的系统。与现有工作中平常的信息传递相比，我们希望层次化机制也可以引入来提升模型的效率和泛化能力。

结论

本文对几何等变图神经网络进行了概述。我们展示了现有工作是我们定义的几何信息传递范式下的特例，包括不可约表示、正则表示和标量化。我们讨论了许多任务上的更广泛的应用前景，包括物理动力学模拟，分子和蛋白质模拟，以及点云数据处理。未来的研究方向颇有希望，我们希望可能跟看到等变GNNs作为一个强大的工具在更多科学领域解决更多问题。